ISIS Application Documentation
jigsaw | Printer Friendly View | TOC | Home |
Improves image alignment by updating camera geometry attached to cubes.
| Overview | Parameters | Example 1 | Example 2 | Example 3 | Example 4 | Example 5 | Example 6 |
DescriptionOverviewThe jigsaw application performs a photogrammetric bundle adjustment on a group of overlapping, level 1 cubes from framing and/or line-scan cameras. The adjustment simultaneously refines the selected image geometry information (camera pointing, spacecraft position) and control point coordinates (x,y,z or lat,lon,radius) to reduce boundary mismatches in mosaics of the images. This functionality is demonstrated below in a zoomed-in area of a mosaic of a pair of overlapping Messenger images. In the before jigsaw mosaic on the left (uncontrolled), the features on the edges of the images do not match. In the after jigsaw mosaic on the right (controlled), the crater edges meet correctly and the seam between the two images is no longer visible. 

The jigsaw application assumes spiceinit or csminit has been run on the input cubes so that camera information is included in the Isis cube labels. In order to run the program, the user must provide a list of input cubes, an input control net, the name of an output control network, and the solve settings. The measured sample/line positions associated with the control measures in the network are not changed. Instead, the control points and camera information are adjusted. jigsaw outputs a new control network that includes the initial state of the points in the network and their final state after the adjustment. The initial states of the points are tagged as a priori in the control network, and their final states are tagged as adjusted. Updated camera information is only written to the cube labels if the bundle converges and the UPDATE parameter is selected. Optional output files can be enabled to provide more information for analyzing the results of the bundle. BUNDLEOUT_TXT provides an overall summary of the bundle adjustment; it lists the user input parameters selected and tables of statistics for both the images and the points. The image statistics can be written to a separate machine readable file with the IMAGESCSV option and likewise for the point statistics with the OUTPUT_CSV option. RESIDUALS_CSV provides a table of the measured image coordinates, the final sample, line, and overall residuals of every control measure in both millimeters and pixels. Observation EquationsThe jigsaw application attempts to minimize the reprojective error within the control network. For each control measure and its control point in the control network, the reprojective error is the difference between the control measure's image coordinate (typically determined from image registration) and the image coordinate that the control point projects to through the camera model. We also refer to the reprojective error as the measure residual. So, for each control measure we can write an observation equation:
reprojective_error = control_measure - camera(control_point)
The camera models use additional parameters such as the instrument position and pointing to compute what image coordinate a control point projects to; so, the camera function in our observation equation can be written more explicitly as:
reprojective_error = control_measure - camera(control_point, camera_parameters)
The primary decision when using the jigsaw application is which parameters to include as variables in the observation equations. Later sections will cover what parameters can be included and common considerations when choosing them. By combining all the observation equations for all the control measures in the control network we can create a system of equations. Then, we can find the camera parameters and control point coordinates that minimize the sum of the squared reprojective errors using the system of equations.
Below is an example system of observation equations for a control network with three images
(A, B, and C) and three control points (1, 2, and 3). Control point 1 has control measures
on images A and B, control point 2 has control measures on images B and C, and control
point 3 has control measures on images A, B, and C. 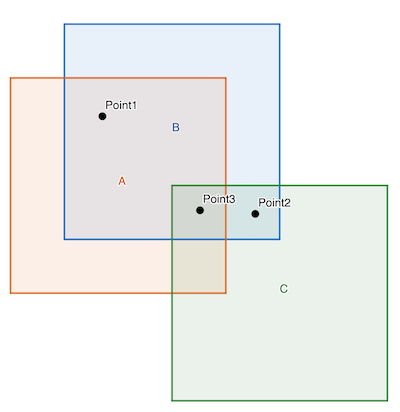
|| control_measure_1_A - camera_A(control_point_1, camera_parameters_A) ||
|| control_measure_1_B - camera_B(control_point_1, camera_parameters_B) ||
|| control_measure_2_B - camera_B(control_point_2, camera_parameters_B) ||
total_error = || control_measure_2_C - camera_C(control_point_3, camera_parameters_C) ||
|| control_measure_3_A - camera_A(control_point_3, camera_parameters_A) ||
|| control_measure_3_B - camera_B(control_point_3, camera_parameters_B) ||
|| control_measure_3_C - camera_C(control_point_3, camera_parameters_C) ||
If the camera projection functions were linear, we could easily minimize this system. Unfortunately, the camera projection functions are quite non-linear; so, we linearize and iteratively compute updates that will gradually approach a minimum. The actual structure of the observation equations is complex and vary significantly based on the dataset and which parameters are being solved for. If the a-priori parameter values are sufficiently far away from a minimum, the updates can even diverge. So, it is important to check your input data set and solve options. Tools like the cnetcheck application and jigsaw options like OUTLIER_REJECTION can help. As with all iterative methods convergence criteria is important. The default for the jigsaw application is to converge based on the sigma0 value. This is a complex value that includes many technical details outside the scope of this documentation. In a brief, it is a measurement of the remaining error in a typical observation. The sigma0 value is also a good first estimate of the quality of the solution. If the only errors in the control network are purely random noise, then the sigma0 should be 1. So, if the sigma0 value for your solution is significantly larger than 1, then it is an indication that there is an unusual source of error in your control network such as poorly registered control measures or poor a-priori camera parameters. Solve OptionsChoosing solve options is difficult and often requires experimentation. As a general rule, the more variation in observation geometry in your dataset and the better distributed your control measures are across and within images, the more parameters you can solve for. The following sections describe the different options you can use when running the jigsaw application. Each section will cover a subset of the options explaining common situations in which they are used and how to choose values for them. Control NetworkControl networks can contain a wide variety of information, but the primary concern for choosing solve options is the presence or lack of ground control. Most control networks are generated by finding matching points between groups of images. This defines a relative relationship between the images, but it does not relate those images to the actual planetary surface; so, additional information is needed to absolutely control the images. In terrestrial work, known points on the ground are identified in the imagery via special target markers, but this is usually not possible with planetary data. Instead, we relate the images to an additional dataset such as a basemap or surface model. This additional relationship is called ground control. Sometimes, there are not sufficient previous data products to provide accurate ground control or ground will be done as a secondary step after successfully running jigsaw on a relatively controlled network. In both these cases, we say that ground control is not present. If your control network does not have ground control, then we recommended that you hold the instrument position fixed and only solve for the instrument pointing. This is because without ground control, the instrument position and pointing can become correlated and there will be multiple minimums for the observation equations. We recommend holding the instrument position fixed because a-priori data for it generally is more accurate than the instrument pointing. Sensor TypesFramingFraming sensors are the most basic type or sensor to use with jigsaw. The entire image is exposed at the same time, so there is only a single position and pointing value for each image. With these datasets you will want to use the either NONE or POSITIONS for the SPSOLVE parameter and ANGLES for the CAMSOLVE parameter. PushbroomPushbroom sensors require additional consideration because the image is exposed over a period of time and therefore, position and pointing are time dependent. The jigsaw application handles this by modeling the position and pointing as polynomial functions of time. Polynomial functions are fit to the a-priori position and pointing values on each image. Then, each iteration updates the polynomial coefficients. Setting CAMSOLVE to velocities will use first degree, linear, polynomials and setting CAMSOLVE to accelerations will use second degree, quadratic, polynomials for the pointing angles. For most pushbroom observations, we recommend using second degree polynomials, solving for accelerations. There are also a variety of parameters that allow for more precise control over the polynomials used and the polynomial fitting process. The OVERHERMITE parameter changes the initial polynomial setup so that it does not replace the a-priori position values. Instead, the polynomial starts out as a zero polynomial and is added to the original position values. This effectively adds the noise from the a-priori position values to the constant term of the polynomial. The OVEREXISTING parameter does the same thing for pointing values. These two options allow you to preserve complex variation like jitter. We recommend enabling these options for jittery images and very long exposure pushbroom images. The SPSOLVE and CAMSOLVE parameters only allow up to a second degree polynomial. To use a higher degree polynomial for pointing values, set CAMSOLVE to ALL and then set the CKDEGREE parameter to the degree of the polynomial you want to fit over the original pointing values and set the CKSOLVEDEGREE parameter to the degree of the polynomial you want to solve for. Setting the SPSOLVE, SPKDEGREE, and SPKSOLVEDEGREE parameters in a similar fashion gives fine control over the polynomial for postion values. For example, if you want to fit a 3rd degree polynomial for the position values and then solve for a 5th degree polynomial set SPSOLVE to ALL, SPKDEGREE to 3, and SPKSOLVEDEGREE to 5. These parameters should only be used when you know the a-priori position and/or pointing values are well modeled by high degree polynomials. Using high degree polynomials can result in extreme over-fitting where the solution looks good in areas near control measures and control points but is poor in areas far from control measures and control points. The end behavior, the solution at the start and end of images, becomes particularly unstable as the degree of the polynomial used increases. Synthetic Aperture RadarRunning the jigsaw application with synthetic aperture radar (SAR) images is different because SAR sensors do not have a pointing component. Thus, you can only solve for the sensor position when working with SAR imagery. SAR imagery also tends to have long duration images which can necessitate using the OVERHERMITE, SPKDEGREE, and SPKSOLVEDEGREE parameters. Parameter SigmasThe initial, or a-priori, camera parameters and control points all contain error, but it is not equally distributed. The jigsaw application allows users to input a-priori sigmas for different parameters that describe how the initial error is distributed. The parameter sigmas are also sometimes called uncertainties. Parameters with higher a-priori sigma values are allowed to vary more freely than those with lower a-priori sigma values. The a-priori sigma values are not hard constraints that limit how much parameters can change, but rather relative accuracy estimates that adjust how much parameters change relative to each other. The POINT_LATITUDE_SIGMA, POINT_LONGITUDE_SIGMA, and POINT_RADIUS_SIGMA parameters set the a-priori sigmas for control points that do not already have a ground source. If a control point already has a ground source, such as a basemap or DEM, then it already has internal sigma values associated with it or is held completely fixed. The exact behavior depends on how the control points were created, a topic outside the scope of this documentation. These sigmas are in meters on the ground, so the latitude and longitude sigmas are uncertainty in meters in the latitude and longitude directions. Generally, you will choose values for these parameters based on the resolution of the images and a visual comparison with other datasets. The radius sigma is also usually higher than the latitude and longitude sigmas because there is less variation of the viewing geometry with respect to the radius. The CAMERA_ANGLES_SIGMA, CAMERA_ANGULAR_VELOCITY_SIGMA, and CAMERA_ANGULAR_ACCELERATION_SIGMA parameters set the a-priori sigmas for the instrument pointing. Similarly, the SPACECRAFT_POSITION_SIGMA, SPACECRAFT_VELOCITY_SIGMA, and SPACECRAFT_ACCELERATION_SIGMA parameters set the a-priori sigmas for the instrument position. The sigma for each parameter is only used if you are solving for that parameter. For example, if you are solving for angular velocities and not solving for any adjustments to the instrument position you would enter CAMERA_ANGLES_SIGMA and CAMERA_ANGULAR_VELOCITY_SIGMA. Finding initial values for these sigmas is challenging as SPICE does not have a way to specify them. Some teams will publish uncertainties for their SPK and CK solutions in separate documentation or the kernel comments, the commnt utility will read the comments on a kernel file. The velocity and acceleration sigmas are in meters per second and meters per second squared respectively (degrees per second and degrees per second squared for angles). So, the velocity sigma will generally be smaller than the position sigma and the acceleration sigma will be smaller than the velocity sigma. Coming up with a-priori sigma values can be quite challenging, but the jigsaw application has the ability to produce updated sigma values for your solution. By enabling the ERRORPROPAGATION parameter, you will get a-posteriori (updated) sigmas for each control point and camera parameter in your solution. This information is helpful for analyzing and communicating the quality of your solution. Computing the updated sigmas, imposes a significant computation and memory overhead, so it is recommended that you enable ERRORPROPAGATION parameter after you have run bundle adjustment with all of your other settings and gotten a satisfactory result. Community Sensor ModelThe jigsaw options that control which parameters to solve for only work with ISIS camera models. When working with community sensor model (CSM) camera models, you will need to manually specify the camera parameters to solve for. This is because the CSM API only exposes a generic camera parameter interface that may or may not be related to the physical state of the sensor when an image was acquired. The CSMSOLVELIST option allows for an explicit list of model parameters. You can also use the CSMSOLVESET or CSMSOLVEYPE options to choose your parameters based on how they are labeled in the model. Each CSM plugin library defines its own set of adjustable parameters. See the documentation for the CSM plugin library you are using for what different adjustable parameters are and when to solve for them. The sigma values for parameters are also included in the CSM plugin library and image support data (ISD). So, you do not need to specify camera parameter sigmas when working with CSM camera models; however, you still need to specify control point coordinate sigmas. For convenience, the csminit application adds information about all of the adjustable parameters to the image label. The CSM API natively uses a rectangular coordinate system. So, we recommend that you have the jigsaw application perform calculations in a rectangular coordinate system when working with CSM camera models. To do this, set the CONTROL_POINT_COORDINATE_TYPE_BUNDLE parameter to RECTANGULAR. You can also set the CONTROL_POINT_COORDINATE_TYPE_REPORTS parameter to RECTANGULAR to see the results in a rectangular coordinate system, but this is a matter of personal preference and will not impact the results. RobustnessMuch of the mathematical underpinning of the jigsaw application expects that the error in the input data is purely random noise. If there are issues with control measures being poorly registered or blatantly wrong, it can produce errors in the output solution. Generally, users should identify and correct these errors before accepting the output of the jigsaw application, but there are a handful of parameters than can be used to make your solutions more robust to them. The OUTLIER_REJECTION parameter adds a simple calculation to each iteration that looks for potential outliers. The median average deviation (MAD) of the measure residuals is computed and then any control measure whose residual is larger than a multiple of the MAD of the measure residuals is flagged as rejected. Control measures that are flagged as rejected are removed from future iterations. The multiplier for the rejection threshold is set by the REJECTION_MULTIPLIER parameter. The residuals for rejected measures are re-computed after each iteration and if they fall back below the threshold they are un-flagged and included again. Enabling this parameter can help eliminate egregious errors in your control measures, but it is not very sensitive. It is also not selective about what is rejected. So, it is possible to introduce islands into your control network when the OUTLIER_REJECTION parameter is enabled. For this reason, always check your output control network for islands with the cnetcheck application when using the OUTLIER_REJECTION parameter. Choosing an appropriate value for the REJECTION_MULTIPLIER is about deciding how aggressively you want to eliminate control measures. The default value will only remove extreme errors, but lower values will remove control measures that are not actually errors. It is recommended that you start with the default value and then if you want to remove more potential outlier, reduce it gradually. If you are seeing too many rejections with the default value, then your input data is extremely poor and you should investigate other methods of improving it prior to running the jigsaw application. You can use the qnet application to examine and improve your control network. You can use the qtie application to manually adjust your a-priori camera parameters. The jigsaw application also has the ability to set sigmas for individual control measures. Similar to the sigmas for control points and parameters, these are a measurement of the relative quality of each control measure. Control measures with a higher sigma have less impact on the solution than control measures with a lower sigma. Most control networks have a large number of control measures and it is not realistic to manually set the sigma for each one. So, the jigsaw application can instead use maximum likelihood estimation (MLE) to estimate the sigma for each control measure each iteration. There are a variety of models to choose from, but all of them start each control measure's sigmas at 1. Then, if the control measure's reprojective error falls beyond a certain quantile the sigma will be increased. This reduces the impact of poor control measures in a more targeted fashion than simple outlier rejection. In order to produce good results, though, a high density of control measures is required to approximate the true reprojective error probability distributions. Some of the modules used with MLE can set a measure's sigma to infinity, effectively removing it from the solution. Similar to when using the OUTLIER_REJECTION parameter, this can create islands in your control network. If you are working with a large amount of data and want a robustness option that is more targeted and customizable than outlier rejection, then using the MLE parameters is a good option. See the MODEL1, MODEL2, MODEL3, MAX_MODEL1_C_QUANTILE, MAX_MODEL2_C_QUANTILE, and MAX_MODEL3_C_QUANTILE parameter documentation for more information. Observation Mode
Sometimes multiple images are exposed at the same time. They could be exposed by different sensors
on the same spacecraft or they could be read out from different parts of the same sensor. When
this happens, many of the camera parameters for the two images are the same. By default, the
jigsaw application has a different set of camera parameters for each image. To allow
different images that are captured simultaneously to share camera parameters enable the
OBSERVATIONS parameter. This will combine all of the images with the same observation
number into a single set of parameters. By default the observation number for an image is the
same as the serial number. For some instruments, there is an extra keyword in their serial number
translation file called ReferencesFor information on what the original jigsaw code was based on checkout Rand Notebook A more technical look at the jigsaw application can be found in Jigsaw: The ISIS3 bundle adjustment for extraterrestrial photogrammetry by K. L. Edmundson et al. A rigorous development of how the jigsaw application works can be found in these lecture notes from Ohio State University. Known IssuesRunning jigsaw with a control net containing JigsawRejected flags may result in bundle failure Solving for the target body radii (triaxial or mean) is NOT possible and likely increases error in the solve. CategoriesRelated Objects and DocumentsApplicationsHistory
|
Parameter GroupsFiles
Solve Options
Maximum Likelihood Estimation
Convergence Criteria
Camera Pointing Options
Spacecraft Options
Community Sensor Model Options
Target Body
Control Point Parameters
Parameter Uncertainties
Output Options
|
Files: FROMLIST
Description
This file contains a list of all cubes in the control network
| Type | filename |
|---|---|
| File Mode | input |
| Filter | *.txt *.lis |
Files: HELDLIST
Description
This file contains a list of all cubes whose orientation and position will be held in the adjustment. These images will still be included in the solution, but their camera orientation and spacecraft position will be constrained to keep the values from changing. This is an optional parameter and the default is to not hold any of the images. Note that held images must not overlap each other to work properly.
| Type | filename |
|---|---|
| File Mode | input |
| Internal Default | none |
| Filter | *.txt *.lis |
Files: CNET
Description
This file is a control network generated from programs such as autoseed or qnet. It contains the control points and associated measures.
| Type | filename |
|---|---|
| File Mode | input |
| Filter | *.net |
Files: ONET
Description
This output file contains the updated control network with the final coordinates of the control points and residuals for each measurement.
| Type | filename |
|---|---|
| File Mode | output |
| Filter | *.net |
Files: LIDARDATA
Description
This file is a lidar point data generated from lrolola2isis.cpp. It contains lidar control points and associated measures for simultaneous images. If lidar point data are used, SPSOLVE must be turned on (anything besides NONE)
| Type | filename |
|---|---|
| File Mode | input |
| Internal Default | none |
| Exclusions |
|
| Filter | *.dat *.json |
Files: OLIDARDATA
Description
This output file contains the adjusted lidar data with the final coordinates of the lidar points and residuals for each measurement.
| Type | filename |
|---|---|
| File Mode | output |
| Internal Default | none |
| Filter | *.dat *.json |
Files: OLIDARFORMAT
Description
Output lidar data file format.
| Type | string | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Default | BINARY | |||||||||
| Option List: |
|
Files: SCCONFIG
Description
This file contains the Camera/Spacecraft parameters to use when processing images from different sensors. This file should be in PVL format. It should contain an object called SensorParameters with one group per spacecraft/instrument combination. The SpacecraftName and InstrumentId keywords in the Instrument group of an image file are used to create the name of each group in the PVL file. The group pertaining to each spacecraft/instrument should contain the keyword/value pairs needed to process images taken with that sensor: CKDEGREE, CKSOLVEDEGREE, CAMSOLVE, TWIST, OVEREXISTING, SPKDEGREE, SPKSOLVEDEGREE, SPSOLVE, OVERHERMITE, SPACECRAFT_POSITION_SIGMA, SPACECRAFT_VELOCITY_SIGMA, SPACECRAFT_ACCELERATION_SIGMA, CAMERA_ANGLES_SIGMA, CAMERA_ANGULAR_VELOCITY_SIGMA, CAMERA_ANGULAR_ACCELERATION_SIGMA. If any of these keywords are missing, then their defaults will be used. There is an example template at $ISISROOT/appdata/templates/jigsaw/SensorParameters.pvl that can be used as a guide.
| Type | filename |
|---|---|
| File Mode | input |
| Exclusions |
|
| Filter | *.pvl |
Solve Options: OBSERVATIONS
Description
This option will solve for SPICE on all cubes with a matching observation number as though they were a single observation. For most missions, the default observation number is equivalent to the serial number of the cube, and a single cube is an observation. However, for the Lunar Orbiter mission, an image has a defined observation number that is a substring of its serial number. This feature allows the three subframes of a Lunar Orbiter High Resolution frame to be treated as a single observation when this option is used; otherwise, each subframe is adjusted independently.
| Type | boolean |
|---|---|
| Default | No |
Solve Options: RADIUS
Description
Select this option to solve for the local radius of each control point. If this button is not turned on, the radii of the points will not change from the cube's shape model.
| Type | boolean |
|---|---|
| Default | No |
| Inclusions |
|
Solve Options: UPDATE
Description
When this option is selected, the application will update the labels of the individual cubes in the FROMLIST with the final values from the solution if the adjustment converges. The results are written to the SPICE blobs attached to the cube, overwriting the previous values. If this option is not selected, the cube files are not changed. All other output files are still created.
| Type | boolean |
|---|---|
| Default | No |
Solve Options: OUTLIER_REJECTION
Description
Select this option to perform automatic outlier detection and rejection.
| Type | boolean |
|---|---|
| Default | No |
| Exclusions |
|
| Inclusions |
|
Solve Options: REJECTION_MULTIPLIER
Description
Rejection multiplier
| Type | double |
|---|---|
| Default | 3.0 |
| Inclusions |
|
Solve Options: ERRORPROPAGATION
Description
Select this option to compute the variance-covariance matrix of the parameters. The parameter uncertainties can be computed from this matrix.
| Type | boolean |
|---|---|
| Default | No |
Maximum Likelihood Estimation: MODEL1
Description
A maximum likelihood estimation model selection.
| Type | string | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Default | NONE | ||||||||||||
| Option List: |
|
Maximum Likelihood Estimation: MAX_MODEL1_C_QUANTILE
Description
The tweaking constant has different meanings depending on the model being used: Huber models: The point at which the transformation motion from L2 to L1 norms takes place. Recommended quantile: 0.5 Welsch model: Residuals whose absolute value is twice the tweaking constant are approaching negligible significance. Recommended quantile: 0.7 Chen model: Residuals whose absolute value is greater than the tweaking constant are totally ignored. Recommended quantile: > 0.9
| Type | double |
|---|---|
| Default | 0.5 |
| Minimum | 0 (exclusive) |
| Maximum | 1 (exclusive) |
Maximum Likelihood Estimation: MODEL2
Description
A maximum likelihood estimation model selection.
| Type | string | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Default | NONE | ||||||||||||||||||
| Option List: |
|
Maximum Likelihood Estimation: MAX_MODEL2_C_QUANTILE
Description
The tweaking constant has different meanings depending on the model being used: Huber models: The point at which the transformation motion from L2 to L1 norms takes place. Recommended quantile: 0.5 Welsch model: Residuals whose absolute value is twice the tweaking constant are approaching negligible significance. Recommended quantile: 0.7 Chen model: Residuals whose absolute value is greater than the tweaking constant are totally ignored. Recommended quantile: > 0.9
| Type | double |
|---|---|
| Default | 0.5 |
| Minimum | 0 (exclusive) |
| Maximum | 1 (exclusive) |
Maximum Likelihood Estimation: MODEL3
Description
A maximum likelihood estimation model selection.
| Type | string | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Default | NONE | ||||||||||||||||||
| Option List: |
|
Maximum Likelihood Estimation: MAX_MODEL3_C_QUANTILE
Description
The tweaking constant has different meanings depending on the model being used: Huber models: The point at which the transformation motion from L2 to L1 norms takes place. Recommended quantile: 0.5 Welsch model: Residuals whose absolute value is twice the tweaking constant are approaching negligible significance. Recommended quantile: 0.7 Chen model: Residuals whose absolute value is greater than the tweaking constant are totally ignored. Recommended quantile: > 0.9
| Type | double |
|---|---|
| Default | 0.5 |
| Minimum | 0 (exclusive) |
| Maximum | 1 (exclusive) |
Convergence Criteria: SIGMA0
Description
Converges on stabilization of Sigma0. Convergence occurs when the change in sigma0 between iterations is less than or equal to Sigma0.
| Type | double |
|---|---|
| Default | 1.0e-10 |
| Minimum | 0 (exclusive) |
Convergence Criteria: MAXITS
Description
Maximum number of times to iterate. The application stops iterating at MAXIT, or when convergence is reached.
| Type | integer |
|---|---|
| Default | 50 |
| Minimum | 1 (inclusive) |
Camera Pointing Options: CKDEGREE
Description
The degree of the polynomial fit to the original camera angles and used to generate a priori camera angles for the first iteration.
| Type | integer |
|---|---|
| Default | 2 |
| Minimum | 0 (inclusive) |
Camera Pointing Options: CKSOLVEDEGREE
Description
The degree of the polynomial being fit to in the bundle adjust solution. This polynomial can be different from the one used to generate the a priori camera angles used in the first iteration. In the case of an instrument with a jitter problem, a higher degree polynomial fit to each of the camera angles might provide a better solution (smaller errors). For framing cameras, the application automatically sets degree to 0.
| Type | integer |
|---|---|
| Default | 2 |
| Minimum | 0 (inclusive) |
Camera Pointing Options: CAMSOLVE
Description
This parameter is used to specify which, if any, camera pointing parameters to include in the adjustment.
| Type | string | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Default | ANGLES | ||||||||||||||||||
| Option List: |
|
Camera Pointing Options: TWIST
Description
If this option is selected, the twist angle will be adjusted in the bundle adjustment solution.
| Type | boolean |
|---|---|
| Default | Yes |
Camera Pointing Options: OVEREXISTING
Description
This option will fit a polynomial over the existing pointing data. This data is held constant in the adjustment, and the initial value for the each of the coefficients in the polynomials is 0. When this option is used, the current pointing is used as a priori in the adjustment.
| Type | boolean |
|---|---|
| Default | No |
Spacecraft Options: SPKDEGREE
Description
The degree of the polynomial fit to the original camera position and used to generate a priori camera positions for the first iteration.
| Type | integer |
|---|---|
| Default | 2 |
| Minimum | 0 (inclusive) |
Spacecraft Options: SPKSOLVEDEGREE
Description
The degree of the polynomial being fit to in the bundle adjust solution. This polynomial can be different from the one used to generate the a priori camera positions used in the first iteration. In the case of an instrument with a jitter problem, a higher degree polynomial fit for the camera position might provide a better solution (smaller errors). For framing cameras, the application automatically sets degree to 0.
| Type | integer |
|---|---|
| Default | 2 |
| Minimum | 0 (inclusive) |
Spacecraft Options: SPSOLVE
Description
This parameter is used to specify which, if any, spacecraft position parameters to include in the adjustment.
| Type | string | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Default | NONE | ||||||||||||||||||
| Option List: |
|
Spacecraft Options: OVERHERMITE
Description
This option will fit a polynomial over the existing Hermite cubic spline used to interpolate the coordinates of the spacecraft position. The spline is held constant in the adjustment, and the initial value for the each of the coefficients in the polynomials is 0. When this option is used, the current positions are used as a priori in the adjustment.
| Type | boolean |
|---|---|
| Default | No |
Community Sensor Model Options: CSMSOLVESET
Description
Specify one of the parameter sets from the CSM GeometricModel API to solve for. All parameters belonging to the specified set will be solved for.
| Type | string | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Internal Default | none | ||||||||||||
| Option List: |
|
||||||||||||
| Exclusions |
|
Community Sensor Model Options: CSMSOLVETYPE
Description
Specify a parameter type from the CSM GeometricModel API to solve for. All parameters of the specified type will be solved for.
| Type | string | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Option List: |
|
|||||||||||||||
| Exclusions |
|
Community Sensor Model Options: CSMSOLVELIST
Description
All CSM parameters in this list will be solved for. Trailing and leading whitespace will be stripped off. Use standard ISIS parameter array notation to specify multiple parameters.
| Type | string |
|---|---|
| Exclusions |
|
Target Body: SOLVETARGETBODY
Description
Solve for target body parameters. The parameters, their a priori values, and uncertainties are input using a PVL file specified by TBPARAMETERS below. An example template PVL file is located at $ISISROOT/appdata/templates/jigsaw/TargetBodyParameters.pvl.
| Type | boolean |
|---|---|
| Default | false |
| Inclusions |
|
Target Body: TBPARAMETERS
Description
This file contains target body parameters to solve for in the bundle adjustment, their a priori values, and uncertainties. The file must be in PVL format. An example template PVL file is located at $ISISROOT/appdata/templates/jigsaw/TargetBodyParameters.pvl. Instructions for the PVL structure are given in the template.
| Type | filename |
|---|---|
| File Mode | input |
| Filter | *.pvl |
Control Point Parameters: CONTROL_POINT_COORDINATE_TYPE_BUNDLE
Description
This parameter indicates which coordinate type will be used to present the control points in the bundle adjustment and bundle output.
| Type | string | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Default | LATITUDINAL | |||||||||
| Option List: |
|
Control Point Parameters: CONTROL_POINT_COORDINATE_TYPE_REPORTS
Description
This parameter indicates which coordinate type will be used to present the control points in the bundle adjustment and bundle output.
| Type | string | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Default | LATITUDINAL | |||||||||
| Option List: |
|
Parameter Uncertainties: POINT_LATITUDE_SIGMA
Description
This optional value will be used as the global latitude uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: POINT_LONGITUDE_SIGMA
Description
This optional value will be used as the global longitude uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: POINT_RADIUS_SIGMA
Description
This value will be used as the global radius uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
| Inclusions |
|
Parameter Uncertainties: POINT_X_SIGMA
Description
This optional value will be used as the global uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: POINT_Y_SIGMA
Description
This optional value will be used as the global uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: POINT_Z_SIGMA
Description
This optional value will be used as the global uncertainty for all points. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: SPACECRAFT_POSITION_SIGMA
Description
This value will be used as the global uncertainty for spacecraft coordinates. Units are meters.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: SPACECRAFT_VELOCITY_SIGMA
Description
This value will be used as the global uncertainty for spacecraft velocity. Units are meters/second.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: SPACECRAFT_ACCELERATION_SIGMA
Description
This value will be used as the global uncertainty for spacecraft acceleration. Units are meters/second/second.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: CAMERA_ANGLES_SIGMA
Description
This value will be used as the global uncertainty for camera angles. Units are decimal degrees.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: CAMERA_ANGULAR_VELOCITY_SIGMA
Description
This value will be used as the global uncertainty for camera angular velocity. Units are decimal degrees/second.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Parameter Uncertainties: CAMERA_ANGULAR_ACCELERATION_SIGMA
Description
This value will be used as the global uncertainty for camera angular acceleration. Units are decimal degrees/second/second.
| Type | double |
|---|---|
| Internal Default | none |
| Minimum | 0 (inclusive) |
Output Options: FILE_PREFIX
Description
File prefix to prepend for the generated output files. Any prefix that is not a file path will have an underscore placed between the prefix and file name.
| Type | string |
|---|---|
| Internal Default | none |
Output Options: BUNDLEOUT_TXT
Description
Selection of this parameter flags generation of the standard bundle output file
| Type | boolean |
|---|---|
| Default | yes |
Output Options: IMAGESCSV
Description
Selection of this parameter flags output of image data (in body-fixed coordinates) to a csv file.
| Type | boolean |
|---|---|
| Default | yes |
Output Options: OUTPUT_CSV
Description
Selection of this parameter flags output of point and image data (in body-fixed coordinates) to csv file.
| Type | boolean |
|---|---|
| Default | yes |
Output Options: RESIDUALS_CSV
Description
Selection of this parameter flags output of image coordinate residuals to a csv file
| Type | boolean |
|---|---|
| Default | yes |
Output Options: LIDAR_CSV
Description
Selection of this parameter flags output of lidar data points to a csv file
| Type | boolean |
|---|---|
| Default | no |
Example 1Solve with CSM parameters Description
This is an example where the cubes in the network have been run through csminit.
When specified in CSMSOLVELIST, parameters described in the CsmInfo group can
be adjusted during the bundle.
Command Line
jigsaw jigsaw fromlis=cubes.lis cnet=input.net onet=output.net radius=yes csmsolvelist="(Omega Bias, Phi Bias, Kappa Bias)" control_point_coordinate_type_bundle=rectangular control_point_coordinate_type_reports=rectangular point_x_sigma=50 point_y_sigma=50 point_z_sigma=50
jigsaw CSM example
|
Example 2Simple run of jigsaw with images from a linescanner DescriptionThis example runs jigsaw in a very simple way using four MRO CTX images. Only the required parameters are entered, with all other parameters left at their default settings. This bundle solution only solves for the camera orientation (see the CAMSOLVE and TWIST parameters). This command does not update the SPICE information attached to the four cubes. A possible use for this simple run would be to test a network to identify control points that are not well placed. Command Line
jigsaw
fromlist=ctx.lis cnet=hand_dense.net onet=hand_dense-jig.net
This command line only sets the three required parameters.
GUI Screenshot
Data FileLinks open in a new window.
|
Example 3Run of jigsaw parameterized for Kaguya Terrain Camera (TC) images and a relative control network covering the Apollo 15 landing site. DescriptionA relative network is a network that connects overlapping images with tie points but has no tie points connected to a ground source. Since there is no connection to ground in the network, this bundle will only solve for camera specific parameters. The bundle could still solve for other parameters and be correct relative to the camera position, but it would increase the complexity of the bundle. The proceeding two examples will include grounded networks, so we will wait to increase the complexity of the bundle until ground points are included. Additionally, in this example we are evaluating the solution and do not want to apply it to the images yet, therefore, update is set to 'no'. This relative bundle turns on and parameterizes the camera twist and camera acceleration solve parameters. Camera twist is a flag that allows the bundle to solve for the camera's rotation around the bore sight axis and uses the same uncertainty estimation as the other two rotations. Setting the camera solve parameter to acceleration, however, does require uncertainties to be set for the angles (deg), angular velocity (deg/s), and angular accelerations (deg/s**2). These values were set with increasing constraint because of the increasing affect alterations of higher order parameters have on the bundle solution. The 'overexisting' flag tells the bundle solution to approximate the camera rotation with a zero polynomial function added to the existing rotation data (adding the polynomial over the existing data). Without the 'overexisting' flag, the bundle fits a polynomial to the existing rotations, throws out the existing data points, and uses the polynomial to calculate the approximate ephemerides when needed. This bundle also lowers the max iterations to 10 (from default 50). Lowering the max iterations does not affect the bundle solution. However, setting a lower iteration limit can serve as a flag if you expect your network to bundle quickly. Finally, the sigma0 convergence criteria was not changed from its default value, it was only explicitly stated in this call. Command Line
jigsaw
fromlist=cubes.lis cnet=relative_reg_jig4_edit.net onet=relative_reg_jig5.net update=no file_prefix=jig5 sigma0=1.0e-10 maxits=10
twist=yes camsolve=accelerations overexisting=yes camera_angles_sigma=.25 camera_angular_velocity_sigma=.1 camera_angular_acceleration_sigma=.01
|
Example 4Run of jigsaw parameterized for Kaguya Terrain Camera (TC) images and an intermediate ground control network covering the Apollo 15 landing site. DescriptionThis example jigsaw bundle is run directly after adding ground control points to the previous relative network. With ground control points inserted into the bundle solution, we will expand the bundle solve parameters to attempt solving for point radius values and the position of the spacecraft. Ground points are weighted more heavily in the bundle than relative control points and adding parameters adds more complexity to the bundle solution. Therefore, it is common to create and refine a network with only relative points and add ground point in after the relative network (and its bundle solution) is of sufficient quality. The purpose of this bundle is to ensure the network bundle converges with the added ground points and solve parameters, before committing to updating the camera pointing on the images, so update is set to 'no'. In addition to the previous solve parameters, this bundle turns on the point radius and spacecraft position solve parameters. Applying the point radius solve parameter requires the point_radius_sigma to be set. This value is a representation the uncertainty (in meters) of the cameras apriori pointing corresponding to the correct elevation on the shape model; this value is not a hard constraint. Often this value can be set, and the appropriateness of the set value can be checked using the 'POINTS DETAIL' section of the bundleout.txt file output by jigsaw. If more than half of the radius total corrections exceed the provided sigma, the uncertainty may need to be increased. Applying the space craft position solve parameter requires an uncertainty estimation through spacecraft_position_sigma (again this value is not a hard constraint). The appropriateness of the provided sigma can be evaluated through the bundleout_images.csv X Correction, Y Correction, and Z Correction columns. The 'overhermite' flag allows an estimation the spacecraft position like the 'overexisting' flag estimates the camera pointing, with a zero-polynomial added over the existing data (for spacecraft position this is a cubic Hermite spline). These options require more memory but provide a solution more representative of small variations in the original ephemeris data. Command Line
jigsaw
fromlist=cubes_for_ground_update.lis cnet=grounded_relative_reg.net onet=grounded_rr_jig1.net update=no file_prefix=jig1rr sigma0=1.0e-10 maxits=10
twist=yes camsolve=accelerations overexisting=yes camera_angles_sigma=.25 camera_angular_velocity_sigma=.1 camera_angular_acceleration_sigma=.01
radius=yes point_radius_sigma=500 spsolve=positions overhermite=yes spacecraft_position_sigma=1000
Data FileLinks open in a new window.
|
Example 5Solve with lidar data Description
This is an example of how to use simultaneous lidar measurments to constrain
the instrument position. The constraints on the lidar data are already contained
in the lidardata input file.
Command Line
jigsaw jigsaw lidar_csv=yes fromlis=cubes.lis cnet=input.net onet=output.net lidardata=lidar_data.json olidardata=lidar_data_jigged.json radius=yes twist=yes camsolve=accelerations overexisting=yes camera_angles_sigma=.25 camera_angular_velocity_sigma=.1
lidar example. Note the lidar_csv, lidardata, and olidardata arguments.
|
Example 6Run of jigsaw parameterized for Kaguya Terrain Camera (TC) images and a final ground control network covering Apollo 15 landing site. DescriptionThis last example is of a final jigsaw run of a grounded network. In this example all network adjustments are done, the bundle is converging, the resulting residuals are acceptable, and therefore we are ready to update the camera pointing on the cubes. During the final run we turn on the error propagation flag, this provides the variance-covariance matrix of the parameters, from which uncertainties can be computed. This is valuable if you plan to compute certainties for your update cubes camera pointing (or any kernels resulting from these updated camera pointings). If you want to double check the update was completed, see cathist or catlab (search for 'Jigged'). Command Line
jigsaw
fromlist=cubes_for_ground_update.lis cnet=grounded_relative_reg.net onet=grounded_rr_jig1_ErrProp.net update=yes file_prefix=jig1rrEP sigma0=1.0e-10 maxits=10
twist=yes camsolve=accelerations overexisting=yes camera_angles_sigma=.25 camera_angular_velocity_sigma=.1 camera_angular_acceleration_sigma=.01
radius=yes point_radius_sigma=500 spsolve=positions overhermite=yes spacecraft_position_sigma=1000 errorpropagation=yes
Data FilesLinks open in a new window.
|