gauss
Filter a cube through a kernel using Gaussian weight
/ x^2+y^2 \
- | ----------- |
G(x,y) = 1 \ 2(STDDEV)^2 /
--------------- e^
2(pi)(STDDEV)^2
This formula creates a kernel that then runs through the image. The center of
the kernel is at (0,0). This means that a 3x3 boxcar will be of the form
The kernel coordinates
(-2,-2) (-1,-2) (0,-2) (1,-2) (2,-2)
(-2,-1) (-1,-1) (0,-1) (1,-1) (2,-1)
(-2, 0) (-1, 0) (0, 0) (1, 0) (2, 0)
(-2, 1) (-1, 1) (0, 1) (1, 1) (2, 1)
(-2, 2) (-1, 2) (0, 2) (1, 2) (2, 2)
The kernel values (approx)
1 4 7 4 1
4 16 26 16 4
7 26 41 26 7 x 1/273
4 16 26 16 4
1 4 7 4 1
Categories
Related Objects and Documents
Applications
History
| Drew Davidson | 2004-08-05 | Original version |
| Drew Davidson | 2004-08-06 | Added application test |
| Drew Davidson | 2004-08-16 | Added examples |
| Drew Davidson | 2005-06-27 | Fixed bug in boxcar size |
| Brendan George | 2006-09-21 | Documentation fixes |
| Kaitlyn Lee | 2018-02-15 | Removed the cout that was outputting e to the terminal. Fixes #5198. |
Parameters
Files
| Type | cube |
|---|---|
| File Mode | input |
| Filter | *.cub |
| Type | cube |
|---|---|
| File Mode | output |
boxcar
| Type | integer |
|---|---|
| Default | 3 |
| Odd | This value must be an odd number |
Standard Deviation
| Type | double |
|---|---|
| Default | 1.0 |
| Minimum | 0 (exclusive) |
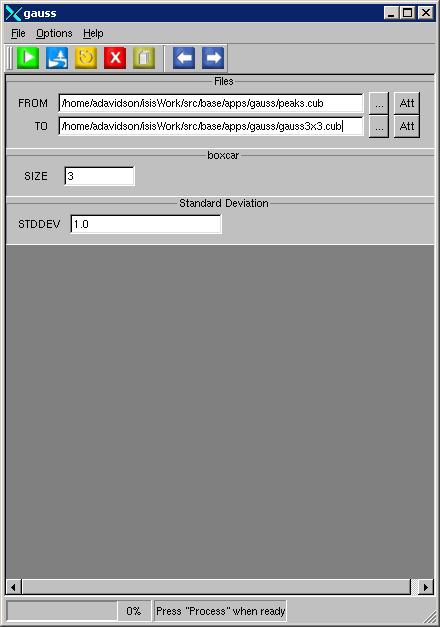
Example 1
Using a 3 x 3 boxcar
Command Line
gauss
from= peaks.cub
to=gauss3x3.cub
size=3
STDDEV= 1.0
GUI Screenshot
Example GUI
gauss guiScreenshot of the GUI with parameters set to perform Gaussian smoothing with a 3 x 3 boxcar.
Input Image
Input image before gauss.
The image before the filter
Parameter Name:
FROM
This is the image as it was taken originally.
Output Image
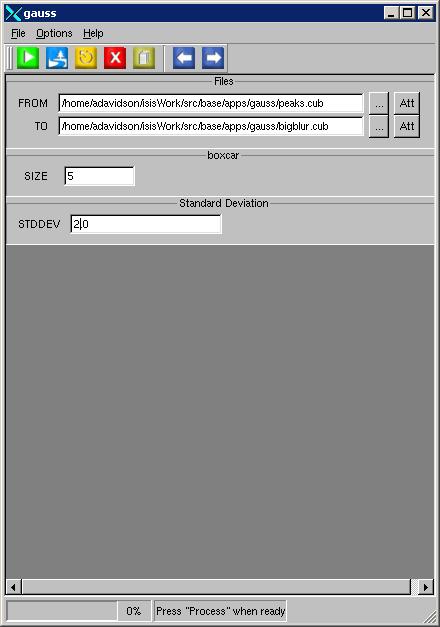
Example 2
Using a 5 x 5 boxcar
Command Line
gauss
from= peaks.cub
to=bigblur.cub
size=5
STDDEV= 2.0
GUI Screenshot
Example GUI
gauss guiScreenshot of the GUI with parameters set to perform Gaussian smoothing with a 5 x 5 boxcar and 2.0 as the standard deviation.
Input Image
Input image before gauss.
The image before the filter
Parameter Name:
FROM
This is the image as it was taken originally.