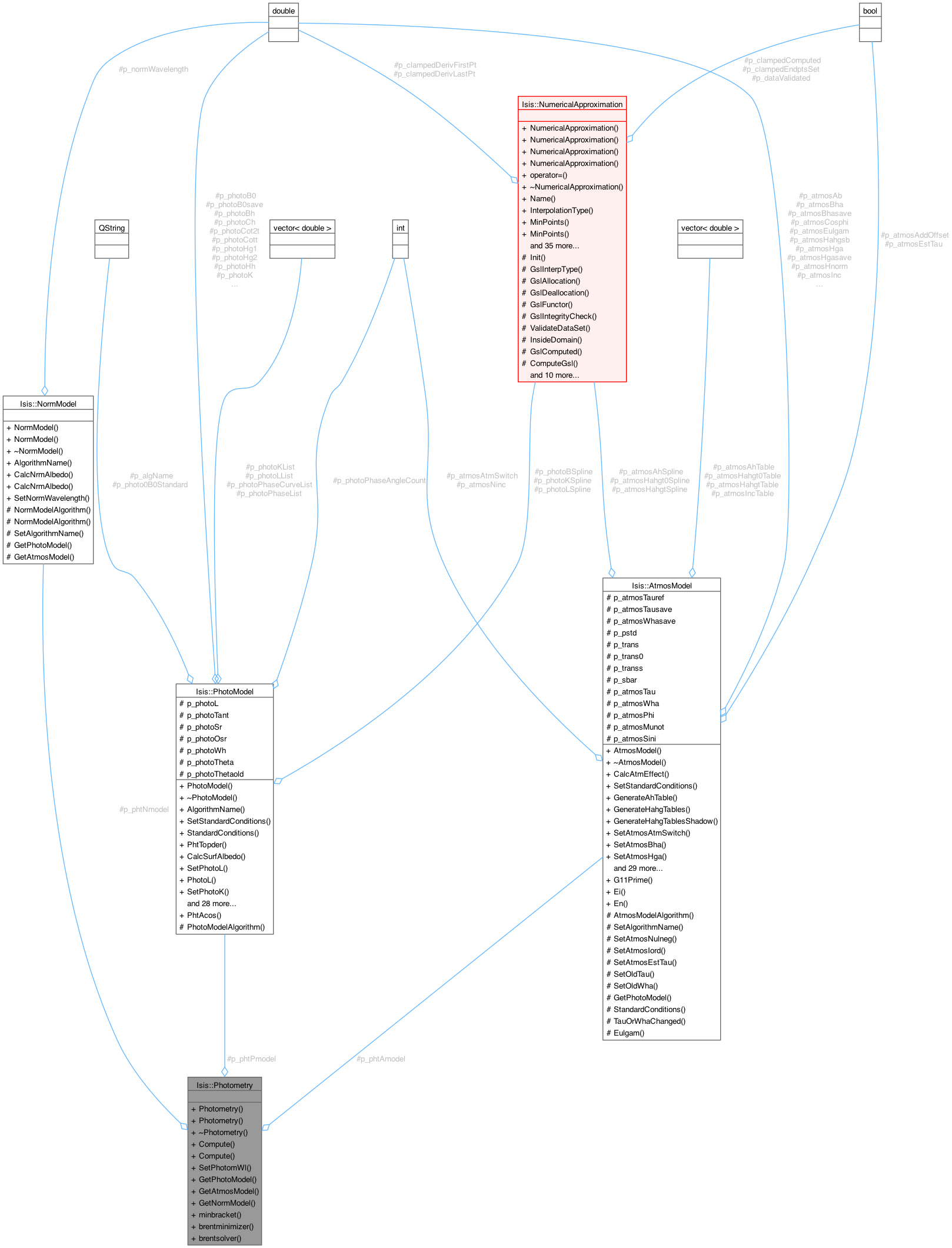
#include <Photometry.h>

Collaboration diagram for Isis::Photometry:

Public Member Functions
	Photometry (Pvl &pvl)
	Create Photometry object.

	Photometry ()

virtual	~Photometry ()
	Destroy Photometry object.

void	Compute (double pha, double inc, double ema, double dn, double &albedo, double &mult, double &base)
	Calculate the surface brightness.

void	Compute (double pha, double inc, double ema, double deminc, double demema, double dn, double &albedo, double &mult, double &base)
	Calculate the surface brightness using ellipsoid and dem.

virtual void	SetPhotomWl (double wl)
	Set the wavelength.

PhotoModel *	GetPhotoModel () const

AtmosModel *	GetAtmosModel () const

NormModel *	GetNormModel () const

Static Public Member Functions
static void	minbracket (double &xa, double &xb, double &xc, double &fa, double &fb, double &fc, double Func(double par, void params), void params)
	Double precision version of bracketing algorithm ported from Python. Solution bracketing for 1-D minimization routine.

static int	brentminimizer (double x_lower, double x_upper, gsl_function *Func, double &x_minimum, double tolerance)
	Brent's method 1-D minimization routine using GSL's r8Brent minimization Algorithm.

static int	brentsolver (double x_lo, double x_hi, gsl_function *Func, double tolerance, double &root)
	GSL's the Brent-Dekker method (Brent's method) combines an interpolation strategy with the bisection algorithm to estimate the root of the quadratic function.

Protected Attributes
AtmosModel *	p_phtAmodel

PhotoModel *	p_phtPmodel

NormModel *	p_phtNmodel

Detailed Description

Author: ????-??-?? Unknown

Constructor & Destructor Documentation

◆ Photometry() [1/2]

Isis::Photometry::Photometry ( Pvl & pvl )

Create Photometry object.

Parameters

pvl	A pvl object containing a valid Photometry specification

See also: photometry.doc

References _FILEINFO_, Isis::PhotoModelFactory::Create(), Isis::AtmosModelFactory::Create(), Isis::NormModelFactory::Create(), p_phtAmodel, p_phtNmodel, p_phtPmodel, and Isis::IException::User.

◆ Photometry() [2/2]

Isis::Photometry::Photometry ( )

inline

◆ ~Photometry()

Isis::Photometry::~Photometry ( )

virtual

Destroy Photometry object.

References p_phtAmodel, p_phtNmodel, and p_phtPmodel.

Member Function Documentation

◆ brentminimizer()

int Isis::Photometry::brentminimizer	(	double	x_lower,
		double	x_upper,
		gsl_function *	Func,
		double &	x_minimum,
		double	tolerance )

static

Brent's method 1-D minimization routine using GSL's r8Brent minimization Algorithm.

The Brent minimization algorithm combines a parabolic interpolation with the golden section algorithm.

This produces a fast algorithm which is still robust. The outline of the algorithm can be summarized as follows: on each iteration Brent's method approximates the function using an interpolating parabola through three existing points. The minimum of the parabola is taken as a guess for the minimum. If it lies within the bounds of the current interval then the interpolating point is accepted, and used to generate a smaller interval. If the interpolating point is not accepted then the algorithm falls back to an ordinary golden section step. The full details of Brent's method include some additional checks to improve convergence.

Author: Sharmila Prasad (8/15/2011)

Parameters

x_lower	- x_lower interval
x_upper	- x_upper interval
Func	- gsl_function, high-level driver for the algorithm Continuous function of one variable for the minimizers to operate on
x_minimum	- x_minimum calculated parabola min value

Returns: double - status

◆ brentsolver()

int Isis::Photometry::brentsolver	(	double	x_lo,
		double	x_hi,
		gsl_function *	Func,
		double	tolerance,
		double &	root )

static

GSL's the Brent-Dekker method (Brent's method) combines an interpolation strategy with the bisection algorithm to estimate the root of the quadratic function.

GSL's the Brent-Dekker method (referred to here as Brent's method) combines an interpolation strategy with the bisection algorithm.

This produces a fast algorithm which is still robust.On each iteration Brent's method approximates the function using an interpolating curve. On the first iteration this is a linear interpolation of the two endpoints. For subsequent iterations the algorithm uses an inverse quadratic fit to the last three points, for higher accuracy. The intercept of the interpolating curve with the x-axis is taken as a guess for the root. If it lies within the bounds of the current interval then the interpolating point is accepted, and used to generate a smaller interval. If the interpolating point is not accepted then the algorithm falls back to an ordinary bisection step.

The best estimate of the root is taken from the most recent interpolation or bisection.

Author: Sharmila Prasad (9/15/2011)

Parameters

x_lo	- Initial lower search interval
x_hi	- Initial higher search interval
Func	- Continuous function of one variable for the root finders to operate on
tolerance	- Root Error Tolerance
root	- Output calculated root

Returns: int - Algorithm status

◆ Compute() [1/2]

void Isis::Photometry::Compute	(	double	pha,
		double	inc,
		double	ema,
		double	deminc,
		double	demema,
		double	dn,
		double &	albedo,
		double &	mult,
		double &	base )

Calculate the surface brightness using ellipsoid and dem.

Returns: Returns the surface brightness

References Isis::NormModel::CalcNrmAlbedo(), and p_phtNmodel.

◆ Compute() [2/2]

void Isis::Photometry::Compute	(	double	pha,
		double	inc,
		double	ema,
		double	dn,
		double &	albedo,
		double &	mult,
		double &	base )

Calculate the surface brightness.

Calculate the surface brightness using only ellipsoid.

Returns: Returns the surface brightness

References Isis::NormModel::CalcNrmAlbedo(), and p_phtNmodel.

◆ GetAtmosModel()

AtmosModel * Isis::Photometry::GetAtmosModel ( ) const

inline

References p_phtAmodel.

◆ GetNormModel()

NormModel * Isis::Photometry::GetNormModel ( ) const

inline

References p_phtNmodel.

◆ GetPhotoModel()

PhotoModel * Isis::Photometry::GetPhotoModel ( ) const

inline

References p_phtPmodel.

◆ minbracket()

void Isis::Photometry::minbracket	(	double &	xa,
		double &	xb,
		double &	xc,
		double &	fa,
		double &	fb,
		double &	fc,
		double	Funcdouble par, void *params,
		void *	params )

static

Double precision version of bracketing algorithm ported from Python. Solution bracketing for 1-D minimization routine.

This bracketing algorithm was taken from http://cxc.harvard.edu/sherpa/methods/fminpowell.py.txt and converted to C++.

References _FILEINFO_, and Isis::IException::User.

◆ SetPhotomWl()

void Isis::Photometry::SetPhotomWl ( double wl )

virtual

Set the wavelength.

Set the wavelength parameter.

This value is obtained from the BandBin Center keyword of the image.

References p_phtNmodel, and Isis::NormModel::SetNormWavelength().

Member Data Documentation

◆ p_phtAmodel

AtmosModel* Isis::Photometry::p_phtAmodel

protected

Referenced by GetAtmosModel(), Photometry(), and ~Photometry().

◆ p_phtNmodel

NormModel* Isis::Photometry::p_phtNmodel

protected

Referenced by Compute(), Compute(), GetNormModel(), Photometry(), SetPhotomWl(), and ~Photometry().

◆ p_phtPmodel

PhotoModel* Isis::Photometry::p_phtPmodel

protected

Referenced by GetPhotoModel(), Photometry(), and ~Photometry().

The documentation for this class was generated from the following files:

/Users/chkim/repos/ISIS3/isis/src/base/objs/Photometry/Photometry.h
/Users/chkim/repos/ISIS3/isis/src/base/objs/Photometry/Photometry.cpp

Public Member Functions

Static Public Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ Photometry() [1/2]

◆ Photometry() [2/2]

◆ ~Photometry()

Member Function Documentation

◆ brentminimizer()

◆ brentsolver()

◆ Compute() [1/2]

◆ Compute() [2/2]

◆ GetAtmosModel()

◆ GetNormModel()

◆ GetPhotoModel()

◆ minbracket()

◆ SetPhotomWl()

Member Data Documentation

◆ p_phtAmodel

◆ p_phtNmodel

◆ p_phtPmodel