Time based linear equation class. More...

#include <Basis1VariableFunction.h>

Inheritance diagram for Isis::Basis1VariableFunction:

Collaboration diagram for Isis::Basis1VariableFunction:

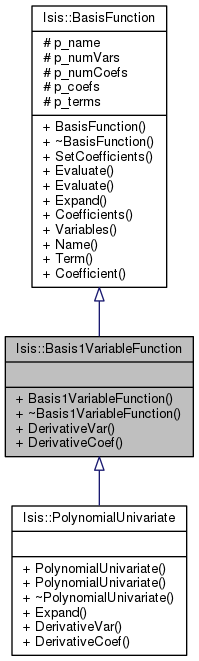
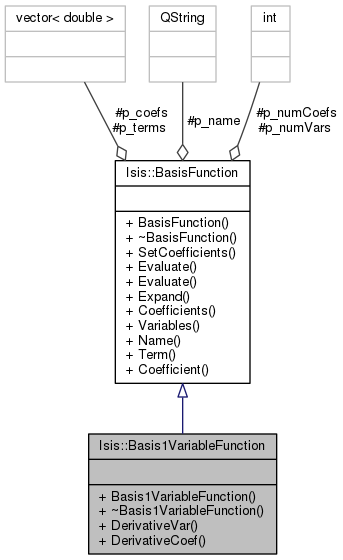
Public Member Functions
	Basis1VariableFunction (const QString &name, int numCoefs)
	Creates a Basis Function with a single variable. More...

virtual	~Basis1VariableFunction ()
	Destroys the Basis1VariableFunction object. More...

virtual double	DerivativeVar (const double value)=0
	This will take the Derivative with respect to the variable and evaluate at given value. More...

virtual double	DerivativeCoef (const double value, const int coefIndex)=0
	Evaluate the derivative defined by the given coefficients with respect to the coefficient at the given index, at the current value. More...

void	SetCoefficients (const std::vector< double > &coefs)
	Set the coefficients for the equation. More...

double	Evaluate (const std::vector< double > &vars)
	Compute the equation using the input variables. More...

double	Evaluate (const double &var)
	Compute the equation using the input variable. More...

virtual void	Expand (const std::vector< double > &vars)
	This is the function you should replace depending on your needs. More...

int	Coefficients () const
	Returns the number of coefficients for the equation. More...

int	Variables () const
	Returns the number of variables in the equation. More...

QString	Name () const
	Returns the name of the equation. More...

double	Term (int c) const
	Returns the cth term. More...

double	Coefficient (int i) const
	Returns the ith coefficient. More...

Protected Attributes
QString	p_name
	The name of the equation. Call it by using Name() More...

int	p_numVars
	The number of variables in the equation. Call it by using Variables() More...

int	p_numCoefs
	The number of coefficients in the equation. More...

std::vector< double >	p_coefs
	A vector of the coefficients in the equation. More...

std::vector< double >	p_terms
	A vector of the terms in the equation. More...

Detailed Description

Time based linear equation class.

This is a class for generating a general one-variable equation for the Isis least squares fitting algorithm (IsisLSQ). It allows the programmer to set up equations in the form of:

\[ x = C1*T1 + C2*T2 + ... + CN*TN; \]

where C1-CN are coefficients and T1-TN are terms with a single variable. For example,

\[ x = C1 + C2*t + C3*t**2 \]

Author: 2004-06-24 Jeff Anderson

Constructor & Destructor Documentation

◆ Basis1VariableFunction()

Isis::Basis1VariableFunction::Basis1VariableFunction	(	const QString &	name,
		int	numCoefs
	)

Creates a Basis Function with a single variable.

Parameters

name	Name of the Basis1VariableFunction. For example, "affine".
numCoefs	Number of coefficients in the equation. For example: \[ x = C1 + C2 * x + C3 * x**2 \] has three coefficients: C1, C2 & C3.

◆ ~Basis1VariableFunction()

virtual Isis::Basis1VariableFunction::~Basis1VariableFunction ( )

inlinevirtual

Destroys the Basis1VariableFunction object.

Member Function Documentation

◆ Coefficient()

double Isis::BasisFunction::Coefficient ( int i ) const

inlineinherited

Returns the ith coefficient.

Parameters

i	The index for the desired coefficient.

Returns: The ith coefficient

References Isis::BasisFunction::p_coefs.

Referenced by Isis::PolynomialUnivariate::DerivativeVar(), Isis::SpicePosition::LoadHermiteCache(), Isis::SurfaceModel::MinMax(), Isis::SpicePosition::SetPolynomial(), Isis::SpiceRotation::SetPolynomial(), and Isis::Affine::Solve().

◆ Coefficients()

int Isis::BasisFunction::Coefficients ( ) const

inlineinherited

Returns the number of coefficients for the equation.

Returns: The number of coefficients.

References Isis::BasisFunction::p_numCoefs.

Referenced by Isis::PolynomialUnivariate::DerivativeCoef(), Isis::PolynomialUnivariate::DerivativeVar(), Isis::SpicePosition::SetPolynomial(), and Isis::SpiceRotation::SetPolynomial().

◆ DerivativeCoef()

virtual double Isis::Basis1VariableFunction::DerivativeCoef	(	const double	value,
		const int	coefIndex
	)

pure virtual

Evaluate the derivative defined by the given coefficients with respect to the coefficient at the given index, at the current value.

Parameters

[in]	value	(const double) value at which to evaluate derivative
[in]	coefIndex	(const int) The index of the coefficient to differentiate with respect to

Returns: (double) The derivative evaluated at given value

Implemented in Isis::PolynomialUnivariate.

◆ DerivativeVar()

virtual double Isis::Basis1VariableFunction::DerivativeVar ( const double value )

pure virtual

This will take the Derivative with respect to the variable and evaluate at given value.

Parameters

[in] value (const double) value at which to evaluate derivative

Returns: (double) The derivative evaluated at given value

Implemented in Isis::PolynomialUnivariate.

◆ Evaluate() [1/2]

double Isis::BasisFunction::Evaluate ( const double & var )

inherited

Compute the equation using the input variable.

Parameters

var	A single double value to use for the equation.

Returns: The output double value resulting from the equation.

References Isis::BasisFunction::Evaluate().

◆ Evaluate() [2/2]

double Isis::BasisFunction::Evaluate ( const std::vector< double > & vars )

inherited

Compute the equation using the input variables.

Parameters

vars	A vector of double values to use for the equation. After setting the coefficients, this can be invoked many times to compute output values given input values.

Returns: The output value.

References _FILEINFO_, Isis::BasisFunction::Expand(), Isis::BasisFunction::p_coefs, Isis::BasisFunction::p_numCoefs, Isis::BasisFunction::p_numVars, Isis::BasisFunction::p_terms, Isis::IException::Programmer, and Isis::toString().

Referenced by Isis::BasisFunction::Evaluate(), Isis::LeastSquares::Evaluate(), Isis::SpiceRotation::EvaluatePolyFunction(), Isis::SpicePosition::LoadHermiteCache(), Isis::SpicePosition::SetEphemerisTimePolyFunction(), and Isis::SpiceRotation::setEphemerisTimePolyFunction().

◆ Expand()

void Isis::BasisFunction::Expand ( const std::vector< double > & vars )

virtualinherited

This is the function you should replace depending on your needs.

It will expand the variables into the terms of the equation. For example,

\[ x = C1 + C2*y + C3*z + C4*y*z \]

must be expanded into the p_terms vector as (1.0, y, z, y*z). Note that the term expansion is not limited, you can use cos, sin, sqrt, abs, etc. This virtual method is automatically invoked by the Evaluate method. We provide a default expansion of p_terms = vars, just a linear combination of the variables.

Parameters

vars	A vector of double values to use for the expansion.

Reimplemented in Isis::PolynomialUnivariate, Isis::PolynomialBivariate, and Isis::NthOrderPolynomial.

References Isis::BasisFunction::p_terms.

Referenced by Isis::BasisFunction::Evaluate().

◆ Name()

QString Isis::BasisFunction::Name ( ) const

inlineinherited

Returns the name of the equation.

Returns: The name of the equation.

References Isis::BasisFunction::p_name.

Referenced by Isis::LeastSquares::AddKnown().

◆ SetCoefficients()

void Isis::BasisFunction::SetCoefficients ( const std::vector< double > & coefs )

inherited

Set the coefficients for the equation.

Parameters

coefs A vector of coefficients for the equation.

References _FILEINFO_, Isis::BasisFunction::p_coefs, Isis::BasisFunction::p_numCoefs, Isis::IException::Programmer, and Isis::toString().

Referenced by Isis::SpiceRotation::DCJdt(), Isis::SpiceRotation::EvaluatePolyFunction(), Isis::SpicePosition::LoadHermiteCache(), Isis::PolynomialUnivariate::PolynomialUnivariate(), Isis::SpicePosition::SetEphemerisTimePolyFunction(), Isis::SpiceRotation::setEphemerisTimePolyFunction(), Isis::SpiceRotation::SetPolynomial(), and Isis::SpicePosition::SetPolynomial().

◆ Term()

double Isis::BasisFunction::Term ( int c ) const

inlineinherited

Returns the cth term.

This is only valid after a Evalute/Expand has been invoked. It represents the expansion of the variables into the ith term. For example,

\[ x = C1 + C2*x + C3*y + C4*x*y \]

would return x*y for the 3rd term (zero-based)

Parameters

c	The index for the desired coefficient.

Returns: The cth term.

References Isis::BasisFunction::p_terms.

◆ Variables()

int Isis::BasisFunction::Variables ( ) const

inlineinherited

Returns the number of variables in the equation.

Returns: The number of variables.

References Isis::BasisFunction::p_numVars.

Referenced by Isis::LeastSquares::AddKnown(), and Isis::NthOrderPolynomial::Expand().

Member Data Documentation

◆ p_coefs

std::vector<double> Isis::BasisFunction::p_coefs

protectedinherited

A vector of the coefficients in the equation.

Call it by using Coefficient()

Referenced by Isis::BasisFunction::Coefficient(), Isis::BasisFunction::Evaluate(), and Isis::BasisFunction::SetCoefficients().

◆ p_name

QString Isis::BasisFunction::p_name

protectedinherited

The name of the equation. Call it by using Name()

Referenced by Isis::BasisFunction::BasisFunction(), and Isis::BasisFunction::Name().

◆ p_numCoefs

int Isis::BasisFunction::p_numCoefs

protectedinherited

The number of coefficients in the equation.

Call it by using Coefficients()

Referenced by Isis::BasisFunction::BasisFunction(), Isis::BasisFunction::Coefficients(), Isis::BasisFunction::Evaluate(), and Isis::BasisFunction::SetCoefficients().

◆ p_numVars

int Isis::BasisFunction::p_numVars

protectedinherited

The number of variables in the equation. Call it by using Variables()

Referenced by Isis::BasisFunction::BasisFunction(), Isis::BasisFunction::Evaluate(), and Isis::BasisFunction::Variables().

◆ p_terms

std::vector<double> Isis::BasisFunction::p_terms

protectedinherited

A vector of the terms in the equation.

Call it by using Term()

Referenced by Isis::BasisFunction::Evaluate(), Isis::BasisFunction::Expand(), Isis::NthOrderPolynomial::Expand(), Isis::PolynomialBivariate::Expand(), Isis::PolynomialUnivariate::Expand(), and Isis::BasisFunction::Term().

The documentation for this class was generated from the following files:

/home/isis3mgr/repos/ISIS3/isis/src/base/objs/Basis1VariableFunction/Basis1VariableFunction.h
/home/isis3mgr/repos/ISIS3/isis/src/base/objs/Basis1VariableFunction/Basis1VariableFunction.cpp

Public Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ Basis1VariableFunction()

◆ ~Basis1VariableFunction()

Member Function Documentation

◆ Coefficient()

◆ Coefficients()

◆ DerivativeCoef()

◆ DerivativeVar()

◆ Evaluate() [1/2]

◆ Evaluate() [2/2]

◆ Expand()

◆ Name()

◆ SetCoefficients()

◆ Term()

◆ Variables()

Member Data Documentation

◆ p_coefs

◆ p_name

◆ p_numCoefs

◆ p_numVars

◆ p_terms