Home

User Documentation

Getting Started
Learn More
Explore in Detail
Get Inspired

Contributor Documentation

Getting Started
Learn More
Explore in Detail
Get Inspired

Quick Links

Software Manual
AstroDiscuss
GitHub
API Reference

Documentation Versions

ISIS 2

Documentation
Tutorials
Technical Documents
USGS

ISIS Application Documentation

shadowtau

Printer Friendly View | TOC | Home

Estimate optical depth (tau) using information from shadow measurements

Overview Parameters

Description

This program estimates the optical depth (tau) values using a table file that consists of measurements collected at different locations on Level1 images with ISIS qview or another image display program. Information for different images can be entered into a single table file. The input values gathered are the average density measurements of a dark shadow and its photometric properties, and the average density of an unshadowed level-surface near the measured dark shadow on a Level1 image that are output to a table file. The table file contains one line per image point of the measured values separated by a comma or space in the following order:

  1. Image ID
  2. Incidence angle of the measured dark shadow
  3. Emission angle of the measured dark shadow
  4. Phase angle of the measured dark shadow
  5. The average DN (radiance) of a level unshadowed area
  6. The average DN (radiance) of a dark shadowed area

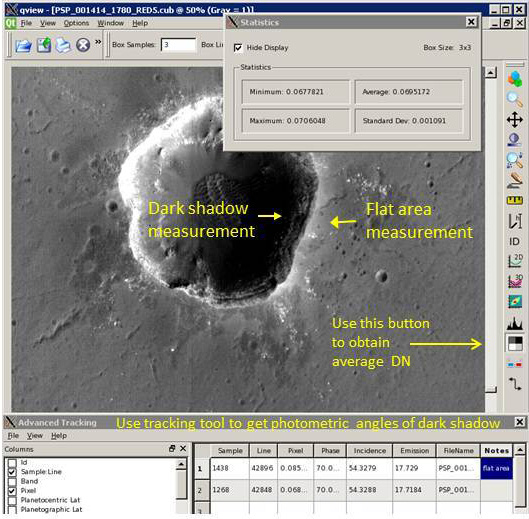
The image below shows an example of areas that could be measured on a Level1 image using the qview tools. The tracking tool is used to obtain the phase, incidence, and emission angles of the dark shadow. The statistics tool in qview is used to obtain the average density of the selected area on a dark shadow and an unshadowed area near the dark shadow. The average pixel values can be added to the tracking window, under notes, for each point, and saved to an output file. Another option is to record the information using a text editor.

QVIEW Example

Whatever method is used to record the information into a table file, the input file to shadowtau must have required column information in a specific order. Note: the program qview does not output the photometric information in the correct order, so the user must modify the output before using the table file in shadowtau.

The following is an example of the input text file after it has been reordered: 

     PSP_001414_1780_RED5.cub, 54.3287, 17.7148, 70.0486, 0.0943, 0.0667265
     PSP_001414_1780_RED5.cub, 54.3283, 17.7173, 70.0506, 0.0926, 0.0653045
     PSP_001414_1780_RED5.cub, 54.3191, 17.7427, 70.0657, 0.0888, 0.069008
     PSP_001414_1780_RED5.cub, 54.3716, 17.7178, 70.0861, 0.0888, 0.0506262
     PSP_001414_1780_RED5.cub, 54.3709, 17.7292, 70.0956, 0.091, 0.0518498

The following is the result of shadowtau; the bolded values are estimated tau and albedo values, respectively:

     PSP_001414_1780_RED5.cub, 54.3287, 17.7148, 70.0486, 0.0943, 0.0667265, 0.43133, 0.120277
     PSP_001414_1780_RED5.cub, 54.3283, 17.7173, 70.0506, 0.0926, 0.0653045, 0.424314, 0.117599
     PSP_001414_1780_RED5.cub, 54.3191, 17.7427, 70.0657, 0.0888, 0.069008, 0.482241, 0.0944602
     PSP_001414_1780_RED5.cub, 54.3716, 17.7178, 70.0861, 0.0888, 0.0506262, 0.307933, 0.134256
     PSP_001414_1780_RED5.cub, 54.3709, 17.7292, 70.0956, 0.091, 0.0518498, 0.311609, 0.138582

For each line in the table file above, the model results for the tau and albedo of the surface are appended to the end of the input line as shown in bold, and exported to the output file. All the results are based on user-selected photometric and atmospheric models, and either the default or user-modified parameter values. Most of the parameters default to appropriate values for Mars red filter images since it is the only other planet with modest atmospheric optical depths besides Earth. The results from the program are useful as an initial value for the "tau" parameter when a photometric correction is applied to the images.

The surface and atmosphere models use the same assumptions as the photomet photometric correction software, so the estimated optical depths are useful for processing images with that program. In other words, the optical depth calculated by this program is model-dependent; however, it is exactly the model-dependent value that will produce the most effective photometric correction in photomet.



SURFACE PHOTOMETRIC FUNCTION MODELS


Available photometric function models and required parameter names
Name Required parameter names
Hapkehen B0, hg1, hg2, hh, theta, wh
Hapkeleg Theta, wh, bh, ch, hh, b0, zerob0st
Lambert None
LommelSeeliger None
LunarLambert L
LunarLambertEmpirical (Disabled until next release) Datafile
LunarLambertMcEwen None
Minnaert K
MinnaertEmpirical (Disabled until next release) Datafile


Photometric model parameter names and settings
Name Description ISIS default Valid range
B0 Hapke opposition surge component 0.0 0 <= value
Bh Hapke Legendre coefficient for single particle phase function 0.0 -1 <= value <= 1
Ch Hapke Legendre coefficient for single particle phase function 0.0 -1 <= value <= 1
Hg1 Hapke Henyey Greenstein coefficient for single particle phase function 0.213 0 <= value <= 1
Hg2 Hapke Henyey Greenstein coefficient for single particle phase function 1.0 0 <= value <= 1
Hh Hapke opposition surge component 0.0 0 <= value
K Minnaert function exponent 0.52 0 <= value
L Lunar-Lambert function weight 0.52 No limit
Theta Hapke macroscopic roughness component 8.0 0 <= value <= 90
Wh Hapke single scattering albedo component 0.52 0 < value <= 1
Zerob0st Flag to set opposition surge B0 to zero True True or False
Datafile Input PVL file for empirical functions None String

The functions are defined as follows, where phase is the phase angle, and u0 and u are the cosines of the incidence and emission angles, respectively:

Lambert
FUNC=u0
LommelSeeliger
FUNC=u0/(u0+u)
Minnaert
FUNC=u0**K * u**(K-1)
LunarLambert (Lunar-Lambert, "lunar" part is Lommel-Seeliger)
FUNC=(1-L)*u0 + 2*L*u0/(u0+u)
MinnaertEmpirical
FUNC=B(phase) * u0**K(phase) * u**(K(phase)-1)
LunarLambertEmpirical
FUNC=B(phase) * ((1-L)*u0 + 2*L*u0/(u0+u))

ATMOSPHERIC PHOTOMETRIC FUNCTION MODELS


Available atmosphereic functions and required parameter names
Function model name Required parameters
Anisotropic1 Bha, hnorm, wha
Anisotropic2 Bha, hnorm, wha
HapkeAtm1 Hga, hnorm, wha
HapkeAtm2 Hga, hnorm, wha
Isotropic1 Hnorm, wha
Isotropic2 Hnorm, wha


Atmospheric models parameter names and settings
Name Description ISIS Default Valid Range
Bha Coefficient of the single particle Legendre phase function 0.95 -1 <= value <= 1
Hga Coefficient of single particle Henyey Greenstein phase function 0.7 -1 < value < 1
Hnorm Atmospheric shell thickness normalized to the planet radius 0.003 0 <= value
Wha Single scattering albedo of atmospheric particles 0.9 0 < value < 1 


References:

Chandrasekhar, S., 1960.  Radiative Transfer. Dover, 393 pp.
Hapke, B. W., 1981. Bidirectional reflectance spectroscopy 1: Theory.
   J. Geophys. Res., pp. 86,3039-3054.
Hapke, B., 1984. Bidirectional reflectance spectroscopy 3: Corrections for
   macroscopic roughness. Icarus, 59, pp. 41-59.
Hapke, B., 1986. Bidirectional reflectance spectroscopy 4: The extinction
   coefficient and the opposition effect. Icarus, 67, pp. 264-280.
Johnson, J. R., et al., 1999, Preliminary Results on Photometric Properties of
   Materials at the Sagan Memorial Station, Mars, J. Geophys. Res., 104, 8809.
Kirk, R. L., Thompson, K. T., Becker, T. L., and Lee, E. M., 2000.
   Photometric modelling for planetary cartography. Lunar Planet. Sci., XXXI,
   Abstract #2025, Lunar and Planetary Institute, Houston (CD-ROM).
Kirk, R. L., Thompson, K. T., and Lee, E. M., 2001. Photometry of the
   martian atmosphere:  An improved practical model for cartography and
   photoclinometry. Lunar Planet. Sci., XXXII, Abstract #1874, Lunar and
   Planetary Institute, Houston (CD-ROM).
McEwen, A. S., 1991. Photometric functions for photoclinometry and other
   applications.  Icarus, 92, pp. 298-311.
Tanaka, K. L., and and Davis, P. A., 1988, Tectonic History of the Syria
   Planum Provice of Mars, J. Geophys. Res., 93, 14,893.
Thorpe, T. E., 1973, Mariner 9 Photometric Observations of Mars from
   November 1971 through March 1972, Icarus, 20, 482.
Tomasko, M. G., et al., 1999, Properties of Dust in the Martian Atmosphere
   from the Imager on Mars Pathfinder, J. Geophys. Res., 104, 8987

Categories

Related Objects and Documents

Applications

History

Randy Kirk1999-11-27 USGS Flagstaff Original Version
Sharmila Prasad & Janet Barrett2011-09-04 Isis3 Original version, shadow_tau ported from isis2 to shadowtau in isis3
Janet Barrett2012-01-05 Tested code to make sure it gives the same results as the ISIS2 version. Created app tests.
Ella Mae Lee2012-11-20 Improve shadowtau documentation, change ZEROB0STANDARD to ZEROB0ST, modified remaining ISIS2 parameter values to ISIS3 values, and disabled the use of a datafile with the empirical functions because of a bug in the program, fixes #455.
Janet Barrett2012-12-07 PLEASE NOTE (in reference to change made on 2012-11-20): The backwards compatibility for the shorter ZEROB0ST parameter name has not been fully implemented in ISIS. As a result, this change has been removed and the full ZEROB0STANDARD parameter name must be used. Support for aliases (deprecated values) must be fully implemented in ISIS before the shorter parameter name (ZEROB0ST) will be available. Fixes #1288.
Lynn Weller2013-02-25 Removed links to applications imbedded in text and replaced with italicized application name. Added application links to the "Related Objects and Documents" section of the documentation. Fixes mantis ticket #1525.
Kimberly Oyama and Janet Barrett2013-04-10 Removed the "NONE" option from the "ATMNAME" parameter because an atmospheric model is required for calculating tau. Fixes #1313.

Parameter Groups

Files

Name Description
FROM Input text file name
TO Output text file name

Photometric Model

Name Description
PHTNAME Photometric model to be used
THETA Macroscopic roughness angle
WH Single scattering albedo
HG1 Hapke Henyey Greenstein coefficient
HG2 Hapke Henyey Greenstein Coefficient
BH Hapke Legendre coefficient
CH Hapke Legendre coefficient
HH Hapke opposition surge
B0 Hapke opposition surge
ZEROB0STANDARD Specifies if opposition surge is set to zero under standard conditions
L Lunar-Lambert function weight
K Minnaert function exponent

Atmospheric Model

Name Description
ATMNAME Atmospheric model to be used
HGA Henyey Greenstein coefficient
WHA Single scattering albedo
BHA Legendre coefficient
HNORM Atmospheric shell thickness
X

Files: FROM

Description

Input text file name with Image ID, incidence, emission, and phase angle of the measured dark shadow, average DN value of flat area and average DN value of a dark shadowed area

Type filename
File Mode input
Filter *.txt
Close Window
X

Files: TO

Description

Output text file name with the input ImageID, incidence, emission, and phase angle of the measured dark shadow, average DN value of flat area, average DN value of a dark shadowed area, plus the estimated tau (optical depth) and albedo (albedo of the surface) values appended to each input line.

Type filename
File Mode output
Filter *.txt
Close Window
X

Photometric Model: PHTNAME

Description

Specify the name of the surface photometric function model to apply to the input image. The available options are the following:

HAPKEHEN
Derive model albedo using the complete Hapke model with Henyey-Greenstein single-particle phase function whose coefficients are hg1 and hg2, plus single scattering albedo wh, opposition surge parameters hh and b0, and macroscopic roughness theta. For a smooth model with opposition effect use theta=0.

The table below shows the Hapke parameters for Mars from Johnson et al. (1999) for IMP data of Photometry Flats (soil) and may be reasonably representative of Mars as a whole. Note that (hg1, hg2=1.0) is equivalent to (-hg1, hg2=0.0).

Parameter settings for Mars
Band Wh B0 Hh Hg1 Hg2
Red 0.52 0.025 0.17 0.213 1.0
Green 0.29 0.29 0.17 0.19 1.0
Blue 0.16 0.995 0.17 0.145 1.0
HAPKELEG
Derive model albedo using complete Hapke model with Henyey Legendre two-term Legendre polynomial phase function whose coefficients are bh and ch, plus single scattering albedo wh, opposition surge parameters hh and b0, and macroscopic roughness theta.
LAMBERT
A simple photometric model which predicts that light incident on a surface is scattered uniformly in all directions; the total amount of reflected light depends on the incidence angle of the illumination. This function does not depend upon the outgoing light direction.
LOMMELSEELIGER
This model takes into account the radiance that results from single scattering (scattering of collimated incident light) and does not take into account the radiance that results from multiple scattering (scattering of diffuse light which has made its way indirectly to the same position by being scattered one or more times). This model depends on the incidence and emission angles.
LUNARLAMBERTMCEWEN
This model was developed specifically for use with the Moon, and designed to be used in conjunction with the Moon(MoonAlbedo) normalization model.
LUNARLAMBERTEMPIRICAL, LUNARLAMBERT, MINNAERTEMPIRICAL, and MINNAERT
These models combine a weighted sum of the LommelSeeliger and Lambert models. Given a suitable value for the LunarLambert function weight, L, these models fit the true reflectance behavior of many planetary surfaces equally well as the Hapke model. These models also depend on the incidence and emission angles.

LUNARLAMBERTEMPIRICAL and MINNAERTEMPIRICAL photometric models, and the parameter name DATAFILE are disabled until the next release. There was a problem using the two functions listed above.

Type combo
Default HAPKEHEN
Internal Default HAPKEHEN
Option List:
Option Brief Description
HAPKEHEN Hapke-Henyey-Greenstein Photometric Model Derive model albedo using complete Hapke model with Henyey-Greenstein single-particle phase function.

Exclusions

  • BH
  • CH
  • L
  • K

Inclusions

  • THETA
  • WH
  • HG1
  • HG2
  • HH
  • B0
  • ZEROB0STANDARD
HAPKELEG Hapke Legendre Polynomial Photometric Model Derive model albedo using complete Hapke model with Henyey Legendre two-term Legendre polynomial phase function.

Exclusions

  • HG1
  • HG2
  • L
  • K

Inclusions

  • THETA
  • WH
  • BH
  • CH
  • HH
  • B0
  • ZEROB0STANDARD
LAMBERT Lambert Photometric Model Simple photometric model which predicts that light incident on a surface is scattered uniformly in all directions.

Exclusions

  • THETA
  • WH
  • HG1
  • HG2
  • HH
  • B0
  • ZEROB0STANDARD
  • BH
  • CH
  • L
  • K
LOMMELSEELIGER Lommel-Seeliger Photometric Model This model takes into account the radiance that results from single scattering (scattering of collimated incident light).

Exclusions

  • THETA
  • WH
  • HG1
  • HG2
  • BH
  • CH
  • HH
  • B0
  • ZEROB0STANDARD
  • L
  • K
LUNARLAMBERTMCEWEN Lunar Lambert-McEwen Photometric Model This model was designed for the Moon to be used in conjunction with the MoonAlbedo normalization model.

Exclusions

  • THETA
  • WH
  • HG1
  • HG2
  • BH
  • CH
  • HH
  • B0
  • ZEROB0STANDARD
  • L
  • K
LUNARLAMBERT Lunar Lambert Photometric Model This model combines a weighted sum of the LommelSeeliger and Lambert models.

Exclusions

  • THETA
  • WH
  • HG1
  • HG2
  • BH
  • CH
  • HH
  • B0
  • ZEROB0STANDARD
  • K

Inclusions

  • L
MINNAERT Minnaert Photometric Model This model combines a weighted sum of the LommelSeeliger and Lambert models.

Exclusions

  • THETA
  • WH
  • HG1
  • HG2
  • BH
  • CH
  • HH
  • B0
  • ZEROB0STANDARD
  • L

Inclusions

  • K
Close Window
X

Photometric Model: THETA

Description

The "macroscopic roughness" of the surface as it affects the photometric behavior, used for Hapkehen or Hapkeleg. This is the RMS slope at scales larger than the distance photons penetrate the surface but smaller than a pixel. See Hapke (1986). The roughness correction, which is evaluated if theta is given any value other than 0.0, but is extremely slow. See Hapke (1986).

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Maximum 90.0 (inclusive)
Close Window
X

Photometric Model: WH

Description

The Hapke single scattering albedo of surface particles, see Hapke (1981).

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (exclusive)
Maximum 1.0 (inclusive)
Close Window
X

Photometric Model: HG1

Description

Asymmetry parameter used in Hapke Henyey Greenstein model for the scattering phase function of single particles in the surface. See Hapke (1981). The two-parameter Henyey Greenstein function is as follows:

P(phase)=(1-hg2) * (1-hg1**2)/(1+hg1**2+2*hg1*cos(phase))**1.5 + hg2 * (1-hg1**2)/(1+hg1**2-2*hg1*cos(phase))**1.5

Type string
Default None Specified
Internal Default None Specified
Minimum -1.0 (exclusive)
Maximum 1.0 (exclusive)
Close Window
X

Photometric Model: HG2

Description

The Hapke Henyey Greenstein coefficient for single particle phase function. The second parameter of the two-parameter Henyey-Greenstein model for the scattering phase function of single particles in the surface. This parameter controls the proportions in a linear mixture of ordinary Heneyey Greenstein phase functions with asymmetry parameters equal to +hg1 and -hg1. See HG1 for the full formula.

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Maximum 1.0 (inclusive)
Close Window
X

Photometric Model: BH

Description

The Hapke Legendre coefficient for single particle phase function. A two-term Legendre polynomial is used for the scattering phase function of single particles in the surface:

P(phase) = 1 + bh * p1(cos(phase)) + ch * p2(cos(phase))
Bh is not to be confused with the Legendre coefficient bha of the phase function for atmospheric particles, used when atmname=anisotropic1 or anisotropic2.

Type string
Default None Specified
Internal Default None Specified
Minimum -1.0 (exclusive)
Maximum 1.0 (exclusive)
Close Window
X

Photometric Model: CH

Description

The Hapke Legendre coefficient for single particle phase function. A two-term Legendre polynomial is used for the scattering phase function of single particles in the surface:

P(phase) = 1 + bh * p1(cos(phase)) + ch * p2(cos(phase))

Type string
Default None Specified
Internal Default None Specified
Minimum -1.0 (exclusive)
Maximum 1.0 (exclusive)
Close Window
X

Photometric Model: HH

Description

The Hapke opposition surge component. The width parameter for the opposition effect for the surface if Hapkehen or Hapkeleg is used. See Hapke (1984).

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Close Window
X

Photometric Model: B0

Description

The Hapke opposition surge component. The magnitude of the opposition effect for the surface if Hapkehen or Hapkeleg is used. See Hapke (1984).

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Close Window
X

Photometric Model: ZEROB0STANDARD

Description

This specifies if the opposition surge component B0 is set to zero during the standard conditions phase. The program will automatically default to "true" if "ZEROB0STANDARD" is not defined by the user.

Type string
Default TRUE
Option List:
Option Brief Description
FALSE B0 will not be set to zero for standard conditions phase This option specifies that the opposition surge B0 will not be set to zero during the standard conditions phase.
TRUE B0 will be set to zero for standard conditions phase This option specifies that the opposition surge B0 will be set to zero during the standard conditions phase.
Close Window
X

Photometric Model: L

Description

The Lunar Lambert function weight that governs limb-darkening in the lunar lambert photometric function:

Func=(1-L)*u0 + 2*L*u0/(u0+u)
The values generally fall in the range from 0 (Lambert function) to 1 (Lommel-Seeliger or "lunar" function).

Type string
Default None Specified
Internal Default None Specified
Close Window
X

Photometric Model: K

Description

The Minnaert function exponent that governs limb-darkening in the Minnaert photometric function:

Func=u0**K * u**(K-1)
The values generally fall in the range from 0.5 ("lunar-like", almost no limb darkening) to 1.0 (Lambert function).

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Close Window
X

Atmospheric Model: ATMNAME

Description

This is the name of the atmospheric photometric function model to be applied;the atmospheric model will be considered when the tau value is calculated. The models ending with "1" use a first order scattering approximation. Those ending with "2" use a second order scattering approximation, and are slower but more accurate than the first order scattering approximation. The atmospheric correction can be used with only three atmospheric normalization models: albedoatm, shadeatm, and topoatm. See Kirk et al. (2001).

The table below are photometric parameter values for Mars, adopted from Tomasko et al. (1999):

Band Wha Hga
Red 0.95 0.68
Blue 0.76 0.78

Type combo
Default HAPKEATM1
Internal Default HAPKEATM1
Option List:
Option Brief Description
ANISOTROPIC1 Anisotropic 1 atmospheric model Uses Chandrasekhar's solution for anisotropic scattering described by a one-term Legendre polynomial.

Exclusions

  • HGA

Inclusions

  • HNORM
  • BHA
  • WHA
ANISOTROPIC2 Anisotropic 2 atmospheric model Uses Chandrasekhar's solution for anisotropic scattering described by a one-term Legendre polynomial.

Exclusions

  • HGA

Inclusions

  • HNORM
  • BHA
  • WHA
HAPKEATM1 Hapke 1 Atmospheric Model A one-term Henyey Greenstein function is used.

Exclusions

  • BHA

Inclusions

  • HNORM
  • HGA
  • WHA
HAPKEATM2 Hapke 2 atmospheric model A one-term Henyey Greenstein function is used.

Exclusions

  • BHA

Inclusions

  • HNORM
  • HGA
  • WHA
ISOTROPIC1 Isotropic 1 atmospheric model Uses Chandrasekhar's solution for isotropic scattering.

Exclusions

  • HGA
  • BHA

Inclusions

  • HNORM
  • WHA
ISOTROPIC2 Isotropic 2 atmospheric model Uses Chandrasekhar's solution for isotropic scattering.

Exclusions

  • HGA
  • BHA

Inclusions

  • HNORM
  • WHA
Close Window
X

Atmospheric Model: HGA

Description

The coefficient of single particle Henyey Greenstein phase function. Henyey-Greenestein asymmetry parameter for atmospheric particle phase function, used in hapkeatm1 and hapkeatm2 atmospheric models. Not to be confused with corresponding parameter hg1 for the surface particles.

Type string
Default None Specified
Internal Default None Specified
Minimum -1.0 (exclusive)
Maximum 1.0 (exclusive)
Close Window
X

Atmospheric Model: WHA

Description

The single scattering albedo of atmospheric particles.

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (exclusive)
Maximum 1.0 (inclusive)
Close Window
X

Atmospheric Model: BHA

Description

The coefficient of the single particle Legendre phase function. Coefficient of p1 (cosine) term of atmospheric particle phase function, used in anisotropic1 and anisotropic2 atmospheric models. Not to be confused with corresponding coefficient bh for the surface particles.

Type string
Default None Specified
Internal Default None Specified
Minimum -1.0 (inclusive)
Maximum 1.0 (inclusive)
Close Window
X

Atmospheric Model: HNORM

Description

The atmospheric shell thickness normalized to the planet radius, used to modify angles to get more accurate path lengths near the terminator (Ratio of scale height to the planetary radius). The hnorm parameter is defined as "0.003" for Mars, which is the only planet for which the atmospheric modes are currently used.

Type string
Default None Specified
Internal Default None Specified
Minimum 0.0 (inclusive)
Close Window